invention CT Scanner

How the CT Scanner was conceived

An attempt to explain how the idea was conceived to extract the data from a cross section of tissue.

It is necessary to start with the simplest sample, even that is complicated.

Imagine a tissue sample as follows:

In this 3x3 sample the density is shown by the colour and by the number in the square.

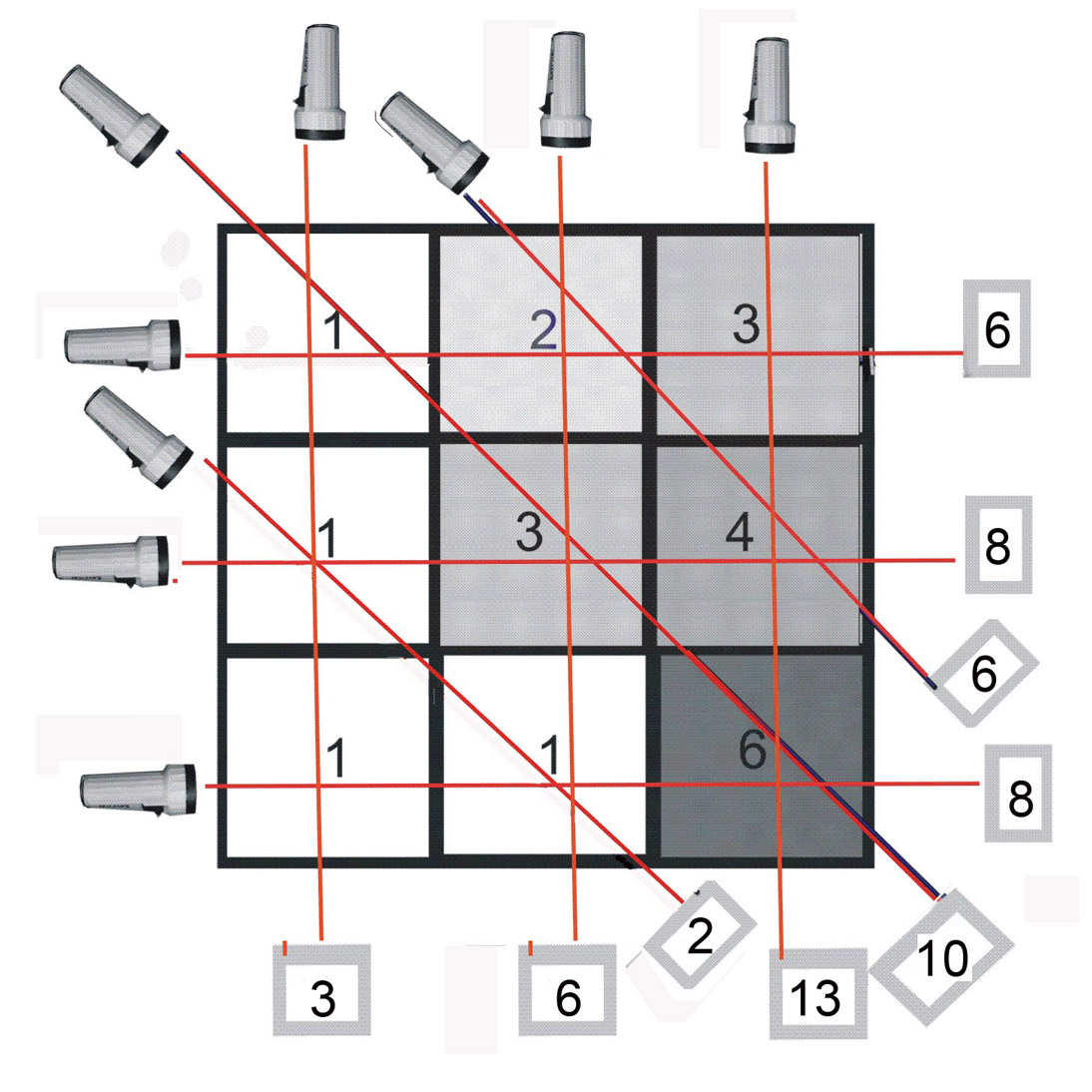
Now we have to shine pencil beams through the sample and collect the amount of light or x-rays transmitted.

In this 3x3 sample the amount of the beam transmitted is collected in the little grey collectors.

At this stage the densities in the nine squares are unknown.

There are nine squares so in this case we need nine simultaneous equations to find the nine unknowns.

Referring back to the picture with the torches, we can see the following:

a+b+c=6

d+e+f=8

g+h+I=8

a+d+g=3

b+e+h=6

c+f+i=13

b+f =6

a+e+i=10

d+h =2

Nine unknowns and nine equations. Now these equations can either be solved longhand or by means of the Excel “Solver” function which can be found under the Excel “tools“ tag. If you don’t have this on your Excel you can download it. Help can be found at http://www.dslimited.biz/excel_tutorials/simultaneouslinearequations.html

But if you don’t want to go to all the trouble to solve the simultaneous equations you can take it from me that they do solve back to the original values which I show at the beginning.

The one thing this does show is that even for a tiny little 3x3 sample there are a lot of equations. So you can just imagine how much calculation would be involved for a high definition sample. It is no wonder that the CT scanner got better over the years as computer power gradually increased.

(My long time colleague has reminded me that the simultaneous equation route is only by way of illustration. In practice it had to be done differently because the presence of noise in the readings meant that there wasn't a perfect solution and so an "iterative" approach was used and generated a picture much more speedily than the conventional way of solving the equations. Later even this was improved by a what he called a "filtered back projection" that was even more efficient! >

Back to Page One